Multilevel Modeling

aML
product info
multilevel example
multiprocess example
A Multilevel Example with Unobserved Heterogeneity
Consider a simple multilevel linear regression model given by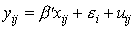
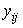 is a continuous outcome of observation
i, replication j. The equation consists of regressors,
is a continuous outcome of observation
i, replication j. The equation consists of regressors,
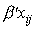 , a residual (heterogeneity) that is common to all
replications,
, a residual (heterogeneity) that is common to all
replications, 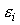 , and an
iid residual,
, and an
iid residual, 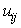 . In aML,
you may specify this model as follows:
. In aML,
you may specify this model as follows:
define regressor set BetaX;
var = <list of variables X>;
define normal distribution; dim=1; name=eps;
define normal distribution; dim=1; name=u;
continuous model;
outcome = y;
model = regressor set BetaX +
residual(draw=1, ref=eps) +
residual(draw=_iid, ref=u);
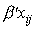 , and two univariate distributions
with residuals eps and u,
corresponding to
, and two univariate distributions
with residuals eps and u,
corresponding to 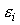 and
and 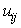 , respectively.
These definitions correspond to estimable model parameters:
, respectively.
These definitions correspond to estimable model parameters:
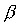 and two standard deviations,
and two standard deviations,
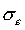 and
and
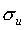 . The regressor set and residuals
were used to specify the model for outcome y
(
. The regressor set and residuals
were used to specify the model for outcome y
(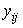 ). The residuals were specified
with "draws," which is aML's approach to indicating which residuals are
correlated with other residuals in potentially large systems of
equations. We specified residual eps with
draw=1, i.e., the same draw (the same
realization) applies to all repeated outcomes. By contrast, we indicated that
residual u is drawn independently
(draw=_iid) for every outcome.
). The residuals were specified
with "draws," which is aML's approach to indicating which residuals are
correlated with other residuals in potentially large systems of
equations. We specified residual eps with
draw=1, i.e., the same draw (the same
realization) applies to all repeated outcomes. By contrast, we indicated that
residual u is drawn independently
(draw=_iid) for every outcome.
How does aML know that there are repeated measures of outcome y, i.e.,
that this is a multilevel model? This is a data issue. When we created the data
(not shown here), outcome variable y was among variables at a lower level of
aggregation. During the estimation stage, the level of a variable is of no concern;
aML will automatically include as many likelihood modules as there are outcome
measures. Explanatory variables 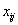 may
be at the same level as
may
be at the same level as 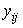 or at more aggregated levels.
or at more aggregated levels.
The example generalizes to all other types of outcomes that aML support, such as durations (hazard models), categorical outcomes (simple/ordered/multinomial probit and logit models), and count outcomes (Poisson, binomial, and negative binomial models). Outcome types may also be mixed, as illustrated in the next example.
To multiprocess example
To download page
Back to product information
Back to home